Je déteste les maths, les maths ça ne sert à rien. Qui parmi nous n'a jamais entendu ou même prononcé ces phrases Cette aversion pour les mathématiques est quasiment devenue un lieu commun dans notre société. Il y a presque une fierté à ne pas les aimer et une personne peut être regardée de travers si elle ose avouer aimer ces dernières.
Mais pourquoi tant de gens ressentent-ils cela Pourquoi les mathématiques, une discipline à la base de tant de progrès humains sont-elles perçues de manière si négative.
La problématique de l'enseignement des mathématiques
Afin de mieux comprendre ce phénomène, arrêtons-nous tout d'abord sur la manière dont cette discipline est enseignée.
Dans son livre "Libérez les mathématiques", Paul Lockhart offre une critique acerbe du système éducatif actuel en matière de mathématiques.

Il décrit comment elles sont souvent réduites à une série de formules et de procédures mécaniques à mémoriser. Imaginez que vous appreniez à peindre en ne faisant que copier des traits de pinceau sans jamais comprendre les nuances des couleurs ou la composition d'une toile. C'est exactement ce qui se passe avec cette matière.
Au lieu d'être un terrain de jeu pour l'imagination et la créativité, elle devient une corvée, un ensemble de règles à suivre sans en saisir le sens profond.
L'enseignement est trop axé sur la mémorisation et l'application mécanique de formules et de procédures sans comprendre leur signification ou leur origine. Selon Lockhart, ce modèle prive les étudiants du plaisir de découvrir par eux-mêmes les concepts mathématiques et d'apprécier la beauté inhérente à la discipline.
Il va même jusqu'à comparer le système actuel à une destruction de l'âme mathématique, transformant une matière potentiellement passionnante en une série de tâches fastidieuses.
Mais cela ne devrait pas être ainsi, les mathématiques pouvant être enseignées de manière à susciter la curiosité et l'enthousiasme. En effet, en faisant découvrir la beauté intrinsèque des mathématiques, la perception qu'en ont les élèves peut être littéralement transformée.
Les mathématiques comme un art
Lockhart propose de considérer les mathématiques comme une forme d'art. Il souligne que comme en musique ou en peinture, celles-ci doivent être une expression de créativité et d'intuition. Pour lui, les mathématiques ne sont pas une discipline froide et mécanique, arguant au contraire qu'elles sont pleines de beauté et de surprise.
Il plaide pour une approche où les étudiants sont encouragés à explorer, à poser des questions et à trouver des solutions de manière inventive et personnelle plutôt que de simplement suivre des instructions préétablies.
L'importance de la découverte
Pour Lockhart, la découverte est au cœur de l'expérience mathématique. Il insiste sur le fait que les élèves devraient être mis au défi de découvrir les principes mathématiques par eux-mêmes à travers des problèmes ouverts et des explorations.
Cette méthode favorise une compréhension plus profonde et plus durable car les élèves s'approprient les concepts et les intègrent de manière significative dans leurs pensées. En un mot, ils deviennent acteurs de leur apprentissage mathématique.
Il utilise des exemples de problèmes mathématiques intrigants et ouverts pour illustrer comment une telle approche peut être mise en œuvre.
L'approche historique
Lockhart suggère également d'enseigner les mathématiques en tenant compte de leur contexte historique.
En effet, en explorant comment et pourquoi certains concepts ont été développés, les élèves sont à même de mieux comprendre les motivations ainsi que les processus de pensée des grands mathématiciens du passé.
Cette approche permet alors d'aborder les mathématiques non pas comme une série de faits établis mais comme une aventure intellectuelle continue pleine de défis et de découvertes. Lockhart est persuadé que cela peut rendre la matière plus vivante et plus engageante pour les étudiants.
Exemple concret
Carl Friedrich Gauss naquit en 1777 en Allemagne. Dès son plus jeune âge, il fut décelé chez lui des signes de génie. Mais c'est à l'école primaire que son talent mathématique se révéla.
Un jour son professeur cherchant à occuper sa classe pendant un moment, demanda à cette dernière de calculer la somme des cent premiers nombres entiers pensant que cela prendrait du temps à la classe, mais il avait sous-estimé le jeune Gauss.
Persuadé que les élèves y consacreraient un certain temps, il fut stupéfait par la rapidité avec laquelle l'élève, alors âgé de dix ans, trouva la solution.
Plutôt que d'additionner les nombres un par un, le jeune garçon vit quelque chose de remarquable puisqu'il comprit que la somme des nombres se simplifiait en regroupant les nombres de manière astucieuse.
Il observa que l'on pouvait couper en deux la liste des nombres de cette manière.

Dans la liste de gauche, on augmente de 1 et dans celle de droite on diminue de 1.
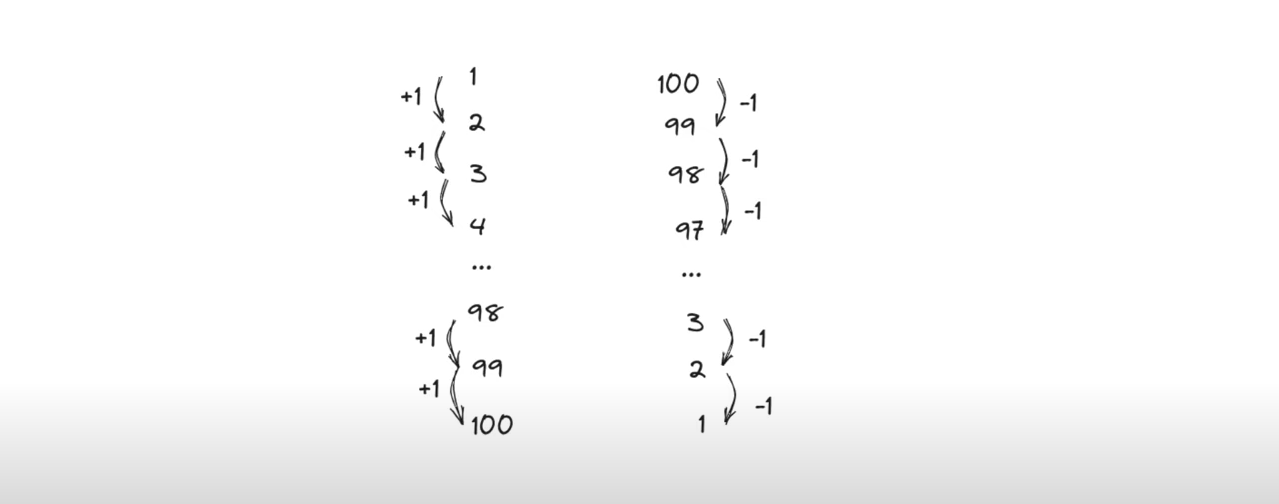
Donc la somme des chiffres de chaque ligne est toujours la même.

Comme chaque liste contient cinquante nombres, le résultat correspond donc à cinq mille cinquante.

Ce principe a même pu être généralisé pour un nombre n d'entiers.
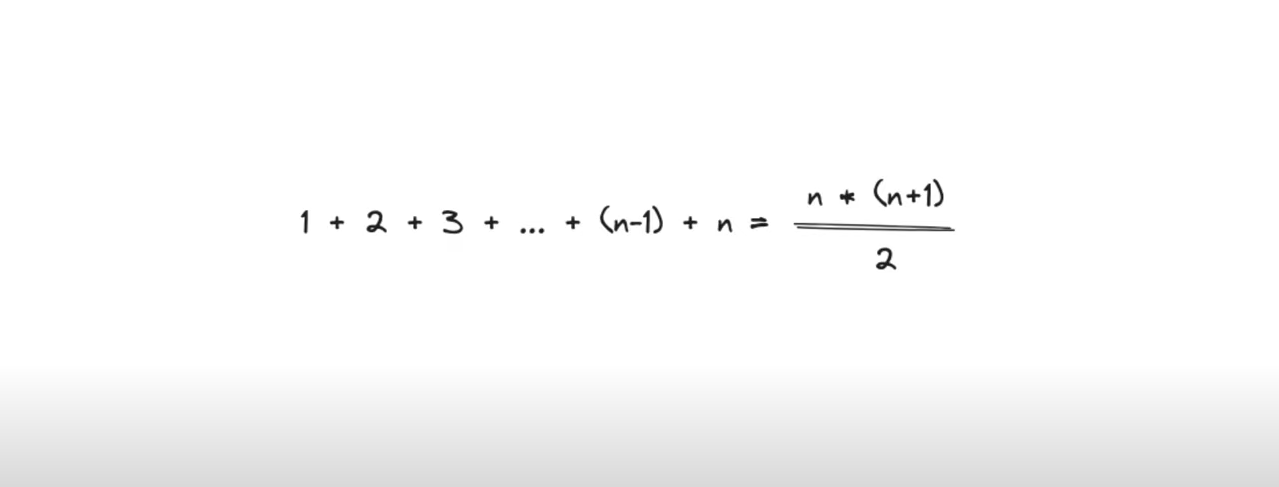
Cet épisode est resté célèbre dans l'histoire des mathématiques, tout en révélant le talent extraordinaire de Gauss.
Il continua à faire des découvertes révolutionnaires tout au long de sa vie, notamment la courbure qui porte son nom.
Ce concept fut utilisé par un certain Einstein dans sa théorie de la relativité générale avec la courbure de l'espace-temps.
Cela montre aussi qu'il existe différentes manières d'aborder les problèmes de mathématiques. Des approches créatives et originales comme celle de Gauss peuvent transformer des calculs en apparence fastidieux en défis passionnant. C'est cette capacité à voir les mathématiques sous un angle nouveau qui les rend fascinantes et accessibles à tous.
Conclusion
alors la prochaine fois que vous entendrez quelqu'un dire qu'il déteste les mathématiques, rappelez-vous, ce ne sont pas les mathématiques qui sont ennuyeuses, mais bien souvent la façon dont elles sont présentées.
De nos jours, de nombreux livres sont disponibles pour voir les mathématiques autrement. Nous pouvons notamment citer celui de Michael Launay, "Le roman des maths" et celui de Manu Houdard, "Very Math Trip".